编者按:环信开源国内首本免费深度学习理论和实战专著《深度学习理论与实战:提高篇 》,内容涵盖听觉,视觉,语言和强化学习,七百多页详尽的理论和代码分析。本文节选自《深度学习理论与实战:提高篇 》一书,原文链接http://fancyerii.github.io/2019/03/14/dl-book/ 。作者李理,环信人工智能研发中心vp,有十多年自然语言处理和人工智能研发经验,主持研发过多款智能硬件的问答和对话系统,负责环信中文语义分析开放平台和环信智能机器人的设计与研发。

Policy Evaluation.ipynb
使用Jupyter Notebook打开Policy Evaluation.ipynb。给定策略计算价值函数的是policy_eval函数,Python代码和伪代码几乎一样:
def policy_eval(policy, env, discount_factor=1.0, theta=0.00001): """ Evaluate a policy given an environment and a full description of the environment's dynamics. Args: policy: shape是[S, A]的矩阵,表示策略 env: OpenAI env对象。 env.P表示环境的转移概率。 每一个元素env.P[s][a]是一个四元组:(prob, next_state, reward, done) theta: 如果所有状态的改变都小于它就停止迭代算法 discount_factor: 打折音子gamma. Returns: V(s),长度为env.nS的向量。 """ # 初始化为零 V = np.zeros(env.nS) while True: delta = 0 # For each state, perform a "full backup" for s in range(env.nS): v = 0 # Look at the possible next actions for a, action_prob in enumerate(policy[s]): # For each action, look at the possible next states... for prob, next_state, reward, done in env.P[s][a]: # Calculate the expected value v += action_prob * prob * (reward + discount_factor * V[next_state]) # How much our value function changed (across any states) delta = max(delta, np.abs(v - V[s])) V[s] = v # Stop evaluating once our value function change is below a threshold if delta < theta: break return np.array(V)
接下来的cell,我们定义一个随机的策略,然后使用上面的函数来计算这个策略的价值函数:
random_policy = np.ones([env.nS, env.nA]) / env.nA v = policy_eval(random_policy, env)
策略提升(Policy Improvement)
我们计算的价值函数的目的是为了找到“更好”的策略。对于给定的策略和状态s,我们知道。如果假设原来的策略是确定的,那么原来的策略是遇到s,会用概率来选择行为a’,同时我们也知道在状态s下采取a并且在后续也使用策略的价值(期望的长期回报)是:
如果这个行为a的价值,那么我们可以这样构造一个新的策略:在状态s时采取固定的策略a,之后的策略和原来的一样。凭直觉是正确的,那怎么证明呢?这个问题可以通过策略提升定理(Policy Improvement Theorem)证明。
策略提升定理
假设和是两个确定的策略(一个状态s下只有一个行为a的概率是1,其余是0),如果对于所有的都有:
那么策略比要“好”,也就是对于所有的:
并且如果第一个不等式是严格大于,那么第二个不等式也是严格大于,也就是一定比更好(而不是一样)。
如果这个定理成立,那就证明了我们前面结论,因为我们新的策略在s的时候采取的满足,而其它的状态s’都是一样的,因此新的策略会更好。当然上面的新策略是随便选择一个满足条件的行为a,但更好的办法是从所有可能的a里选择最大的那个a,此外我们可以改变所有s的策略,而不是一个s,这个改进版本就是我们最终用到的策略提升算法。如果所有的状态,当前的a已经是中最大的那个呢?那说明当前策略已经是最优的策略了。下面我们来证明这个定理:
上面的证明就是不停的应用假设条件,里面有一点就是,因为求一次期望之后就和无关了,可以认为是常量了。
前面说了,我们最终使用的策略是“贪心”的策略,对于所有的s,我们都选择最大的那个a。具体用数学语言来描述就是:
上面的是没有下标的,因为给定时,和是与无关的。当和一样好的时候,,我们代入上面第一个等式得到:
这就是贝尔曼方程,因此如果策略无法提升时就说明我们找到了最优的策略。前面证明的是确定策略的提升,对于随机的策略,也有类似的结论。如果有多个a对应的值都是最大值,那么我们可以随便选择哪个策略。比如,那么提升的策略可以是,也可以是。只要它们的概率加起来等于1就行了。策略提升的代码会和下一节一起实现。
策略迭代(Policy Iteration)
有了前面两节的结论,那么我们可以使用如下方法得到最优策略:随机生成初始策略,然后用策略评估得到,然后用策略提升得到,然后不断重复这个过程就可以得到最优的策略:
上面的过程就是策略迭代(Policy Iteration)。由于有限MDP的策略个数是有限的,因此上面的算法最终会在有限步结束。算法伪代码如下图所示。

图:策略迭代算法伪代码
策略迭代代码示例
我们仍然使用Grid World任务来演示策略迭代算法的实现。用Jupyter notebook打开Policy Iteration.ipynb。
def policy_improvement(env, policy_eval_fn=policy_eval, discount_factor=1.0): """ 策略迭代算法 参数: env: OpenAI环境 policy_eval_fn: 策略评估函数,可以用上一个cell的函数,它有3个参数:policy, env, discount_factor. discount_factor: 大致因子gamma 返回: 一个二元组(policy, V). policy是最优策略,它是一个矩阵,大小是[S, A] ,表示状态s采取行为a的概率 V是最优价值函数 """ # 初始化策略是随机策略,也就是状态s下采取所有行为a的概率是一样的。 policy = np.ones([env.nS, env.nA]) / env.nA while True: # 评估当前策略 V = policy_eval_fn(policy, env, discount_factor) policy_stable = True # For each state... for s in range(env.nS): # 当前策略下最好的action,也就是伪代码里的old-action chosen_a = np.argmax(policy[s]) # 往后看一步找最好的action,如果有多个最好的,随便选一个 action_values = np.zeros(env.nA) for a in range(env.nA): for prob, next_state, reward, done in env.P[s][a]: action_values[a] += prob * (reward + discount_factor * V[next_state]) best_a = np.argmax(action_values) # 贪心的更新policy[s],最佳的a概率是1,其余的0. if chosen_a != best_a: policy_stable = False policy[s] = np.eye(env.nA)[best_a] if policy_stable: return policy, V
读者可以对照伪代码阅读上面的算法,其中最关键的代码是:
for a in range(env.nA): for prob, next_state, reward, done in env.P[s][a]: action_values[a] += prob * (reward + discount_factor * V[next_state]) best_a = np.argmax(action_values)
读者可以对照公式,首先计算所有的,然后选择最大的那一个。回忆一下,env.P[s][a]返回的是所有的(),也就是给定s和a,所有可能的状态s’和奖励r的组合。
还有一点需要注意的就是:我们并没有“显示”的定义当前策略(或者新策略),我们只需要更新policy[s][a]就行了。如果状态是s,那么当前的策略就是从中选择值最大的下标a。最后我们使用策略迭代来求最优策略与最优价值函数:
policy, v = policy_improvement(env)
我们发现它找到了最优的策略:
Reshaped Grid Policy (0=Up, 1=Right, 2=Down, 3=Left): [[U L L D] [U U U D] [U U R D] [U R R U]]
同时它也找到了最优的价值函数:
[[ 0. -1. -2. -3.] [-1. -2. -3. -2.] [-2. -3. -2. -1.] [-3. -2. -1. 0.]]
价值迭代(Value Iteration)
策略迭代的一个问题就是每一次策略的提升都需要计算新策略的价值,计算一个策略的价值本身又需要一次迭代算法。我们有必要精确的知道吗?实际上可能是不需要的,假设策略评估需要100次迭代,那么我们能否只迭代50次就开始策略提升呢?答案是肯定的。更加极端的是只进行一次策略评估就进行策略提升,这就是本节的算法——价值迭代。因为只有一次策略评估,我们可以把它整合到策略提升的公式里,这样看起来我们一种在更新价值,所以这个算法就叫价值迭代:
它的算法伪代码如下图所示。

图:价值迭代算法伪代码
价值迭代代码示例
完整代码在Value Iteration.ipynb。主要代码如下:
def value_iteration(env, theta=0.0001, discount_factor=1.0): """ 价值迭代算法 参数: env: OpenAI environment。env.P代表环境的转移概率p(s',r|s,a) theta: Stopping threshold discount_factor: 打折因子gamma 返回值: 二元组(policy, V)代表最优策略和最优价值函数 """ def one_step_lookahead(state, V): """ 给定一个状态,根据Value Iteration公式计算新的V(s) 参数: state: 状态(int) V: 当前的V(s),长度是env.nS 返回: 返回新的V(s) """ A = np.zeros(env.nA) for a in range(env.nA): for prob, next_state, reward, done in env.P[state][a]: A[a] += prob * (reward + discount_factor * V[next_state]) return A V = np.zeros(env.nS) while True: delta = 0 for s in range(env.nS): # Do a one-step lookahead to find the best action A = one_step_lookahead(s, V) best_action_value = np.max(A) # Calculate delta across all states seen so far delta = max(delta, np.abs(best_action_value - V[s])) # Update the value function V[s] = best_action_value # Check if we can stop if delta < theta: break # Create a deterministic policy using the optimal value function policy = np.zeros([env.nS, env.nA]) for s in range(env.nS): # One step lookahead to find the best action for this state A = one_step_lookahead(s, V) best_action = np.argmax(A) # Always take the best action policy[s, best_action] = 1.0 return policy, V
请读者对照伪代码阅读,细节就不赘述了。
通用策略迭代(Generalized Policy Iteration/GPI)
我们可以把上述的方法总结为通用策略迭代框架(GPI),如下图右所示。策略迭代可以分为两个过程:策略评估和策略提升。它们是轮流进行的,首先进行策略评估然后用策略提升得到更好的策略。策略评估可以通过多次迭代得到准确的评估也可以通过少量(甚至一次)迭代得到粗略的评估。如如下图左所示,我们可以把GPI看成两个约束的优化问题,策略评估把它往上面那条线垂直的拉,使得我们可以更加准确的估计策略的Value;而策略提升把它往下拉,使得策略的价值不断提高。
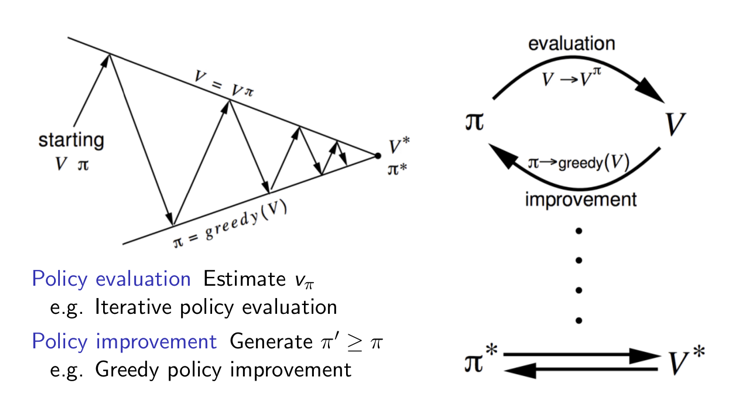
图:通用策略迭代


