通常在开始学编程的时候,你会接触一些常用数据结构。到最后一般会学到哈希表。对于修读计算机科学学位的朋友,你通常要上专门的数据结构课,从了解有关链表、队列和栈的各种知识。这些统称为线性数据结构,因为依逻辑次序从头排到尾。
当你开始进入下一阶段,学习树和图结构时,事情就会显得比处理线性数据结构复杂很多。这促使我们专门写一篇文章来探讨“树”这种特定的数据结构帮大家答疑解惑。
本文内容包括:
树的定义树的结构工作原理代码实现
现在就开始学习吧 :)
树的定义
通常对编程新手来说,线性数据结构比树和图要更好理解。我们此处所说的树,即是以层次化方式组织和存放数据的特定数据结构。
实例解析
为了理解“层次化”的意思,我们以家谱为例:里面有祖父母、父母、孩子、兄弟姐妹。这就是用层次化的模式来构建家谱。
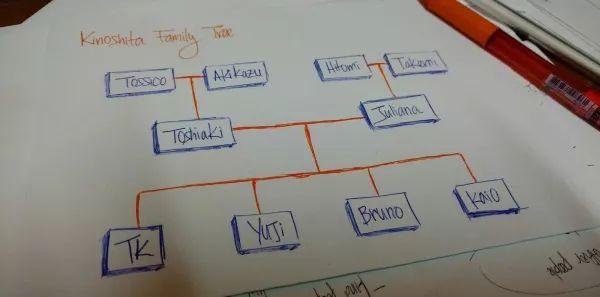
上图就是我的家谱。Tossico,Akikazu,Hitomi和Takemi作为我的祖父母和外祖父母处于最顶层。Toshiaki 和 Juliana是我父母。TK,Yuji,Bruno 和 Kaio 则是我和我的的兄弟姐妹们。
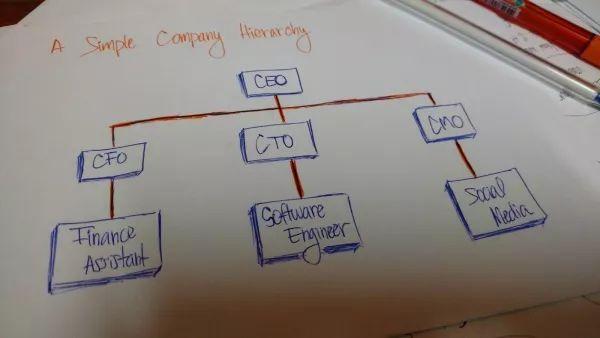
公司组织也是类似的层次化结构
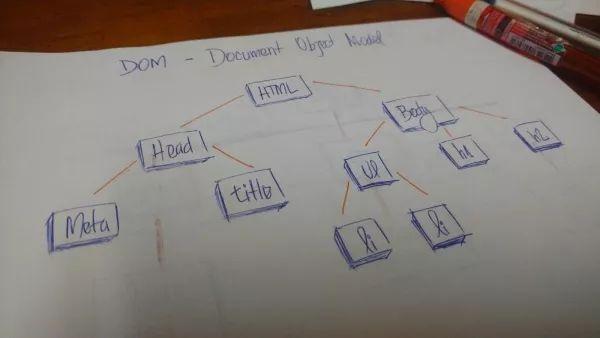
HTML的文档模型对象 (DOM) 就是一棵树最顶层 HTML 标签连接到 head 标签和 body 标签。二者又有对应的子标签,比如 head 含有 meta 和 title 标签,body 含有与可视化内容相关的 h1, a, li等标签。名词定义
树(tree):是以边(edge)相连的结点(node)的集合,每个结点存储对应的值(value/data),当存在子结点时与之相连。
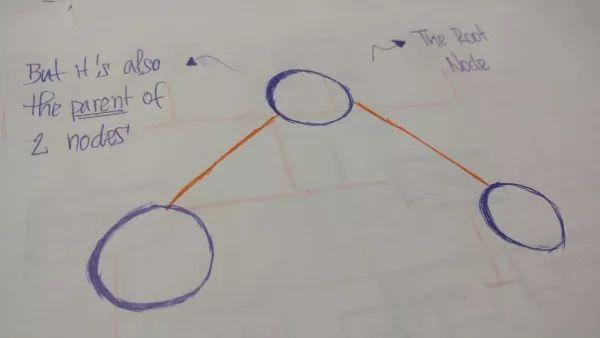
根结点(root):是树的首个结点,在相连两结点中更接近根结点的成为父结点(parent node),相应的另一个结点称为子结点(parent node)。
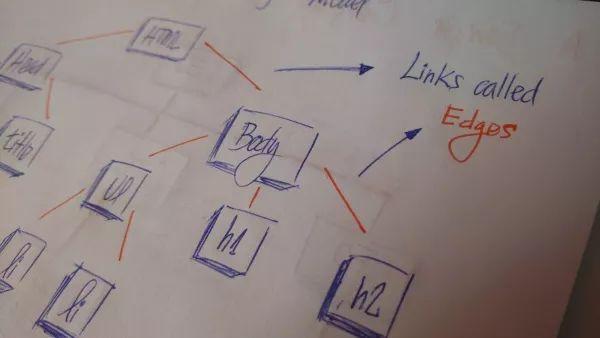
边(edge):所有结点都由边相连,用于标识结点间的关系。边是树中很重要的一个概念,因为我们用它来确定节点之间的关系。
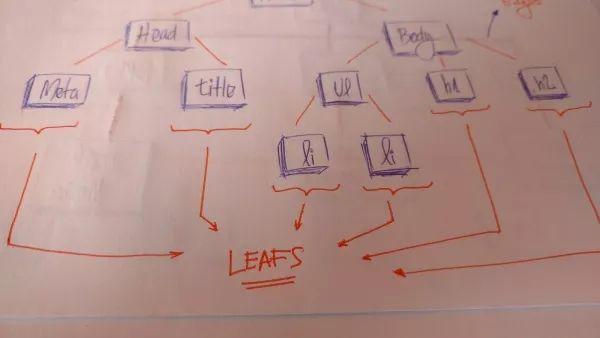
叶子结点(Leaves):是树的末端结点,他们没有子结点,就像真实的树那样 ,由根开始,伸展枝干,到叶为止。
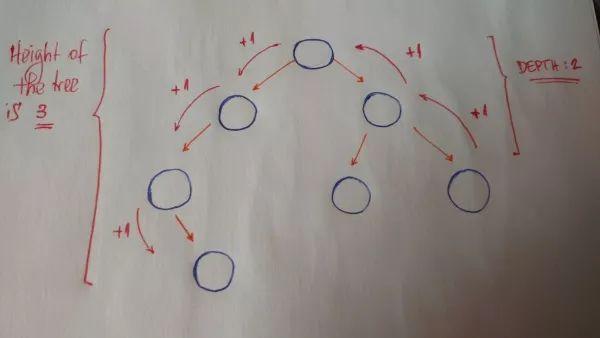
树高(height)与结点深度(depth)也是很重要的概念。树高:是由根结点出发,到子结点的最长路径长度。结点深度:是指对应结点到根结点路径长度。
二叉树
现在来探讨一种特殊的树结构-二叉树(binary tree),它每个节点最多有两个子结点,亦称左孩子和右孩子。
在计算机科学中,二叉树是一种“树”数据结构,树上的每个节点最多有两个孩子,分别为左孩和右孩。——维基百科
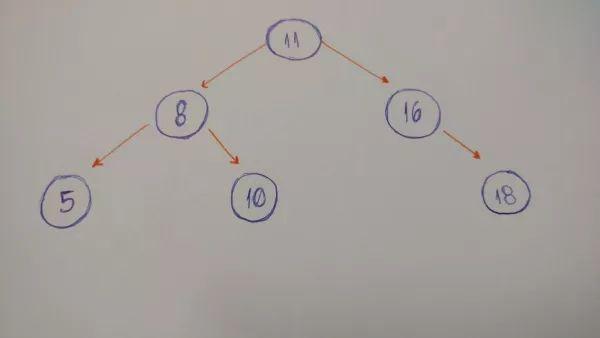
来看一个二叉树的实例。
动手写二叉树
首先明确我们要实现的对象是一个结点集合,每个结点有三个属性:值(value), 左孩子(left_child)和右孩子(right_child)。
写出来会是这个样子:

我们写了一个BinaryTree类,在初始化实际对象的时候传入对应值,并在此时还没有子结点的情况下将左右孩子设为空。
为什么要这么做呢?
因为当我们创建节点的时候,它还没有孩子,我们只有节点数据。
让我们测试一下:

下面到了插入结点的操作:在树还没有对应子结点时新建结点,并赋值给现有结点对应变量。否则,新建结点连接并替换掉现有位置子结点。
画出来是这个样子:

相应代码(左右相同):

为了进一步测试,让我们构建一个更复杂一些的树:
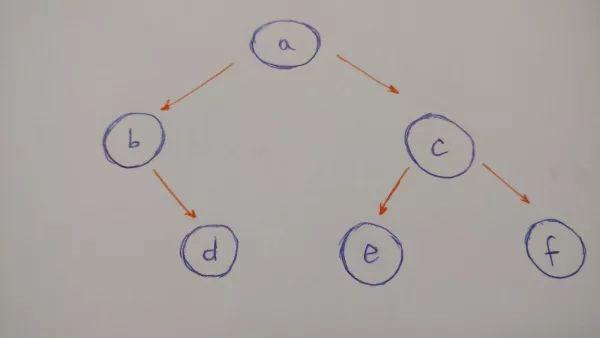
这棵树共有六个结点,其中结点b没有左孩子。对应初始化并插入结点的代码如下:

下一步让我们看看如何对树进行遍历。
一般来讲我们有两种遍历方式:深度优先遍历(DFS)和 广度优先遍历(BFS),前者沿着特定路径遍历到根结点再转换临近路径继续遍历,后者逐层遍历整个树结构。来看具体的例子:
深度优先遍历 (DFS)
DFS会沿特定路径遍历到叶子结点再回溯 (backtracking)进入临近路径继续遍历。以下面的树结构为例:
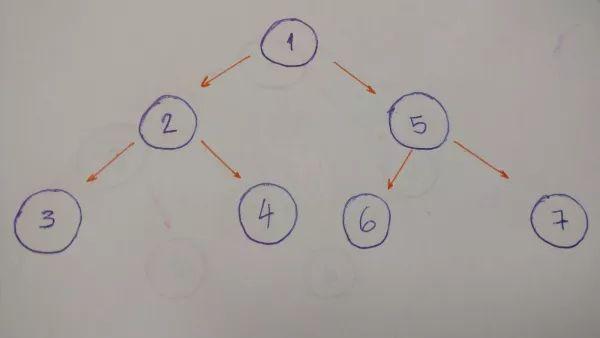
遍历顺序为1–2–3–4–5–6–7
具体来讲,我们会先访问根结点1再访问其左孩子2,接着是2的左孩子3,到达叶子结点回溯一步,访问2的右孩子4,进一步回溯,继续顺序访问5,6和7。在输出遍历结果时,据父结点值相对子结点输出顺序的不同,深度优先遍历又可细分为先序、中序和后序遍历三种情况。
先序遍历
即直接按照我们对结点的访问顺序输出遍历结果即实现,父结点值被最先输出。代码:

中序遍历

中序遍历输出结果为:3–2–4–1–6–5–7。
左孩子值最先输出,然后是父结点,最后是右孩子。对应代码如下:

后序遍历

后序遍历输出结果为:3–4–2–6–7–5–1.
左右孩子值依次输出,最后是父结点,对应代码如下:

广度优先搜索 (BFS)
BFS:按照结点深度逐层遍历树结构。
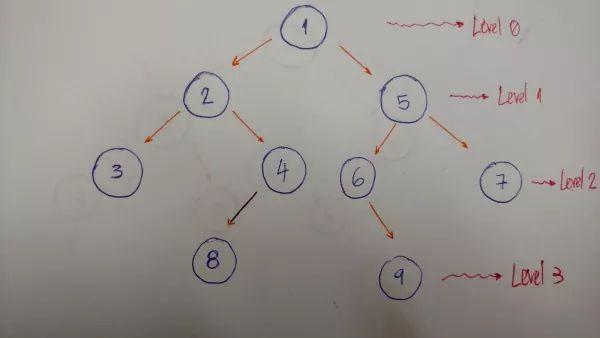
再拿上面的图来实际解释这种方法:

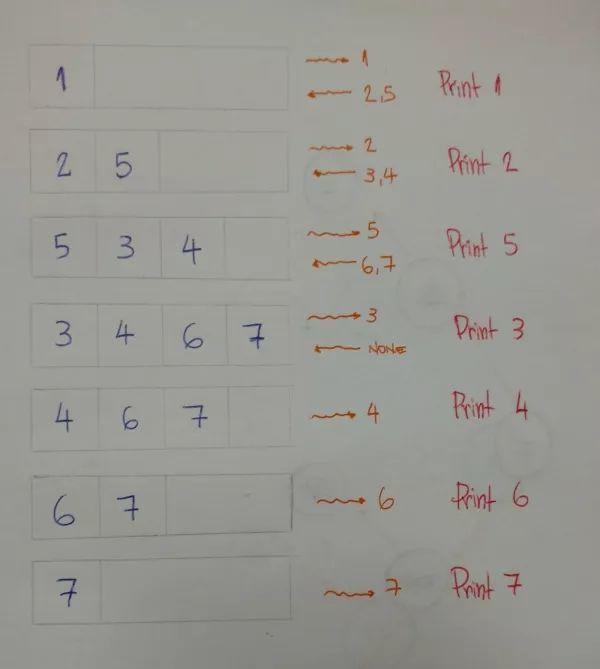
逐层每层从左到右进行遍历,对应遍历结果为:1–2–5–3–4–6–7。对应代码如下:

你应该已经注意到了,我们要借助先进先出(FIFO)的队列(queue)结构完成操作,具体的出入队列顺序如下图所示:
二叉搜索树
二叉搜索树又名有序二叉树,结点元素按固定次序排布,使得我们可以在进行查找等操作时使用二分搜索提高效率。——维基百科
它最明显的特征是父结点值大于左子树任意结点值,小于右子树任意结点值。
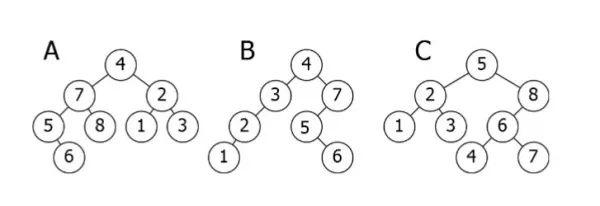
上图以三个二叉树为例,哪个才是正确的呢?
A 左右子树需要进行交换。B 满足条件,是二叉搜索树。C 值为4的结点需要移至3的右孩子处
接下来进行二叉搜索插入、结点检索、结点删除以及平衡的解释。
插入
假设以这种顺序插入结点: 50, 76, 21, 4, 32, 100, 64, 52。50会是我们初始的根结点。

再依次进行如下操作:
76 大于50,置于右边21 小于 50, 置于左边4 置于21左边
最终一气呵成我们会得到下面这棵树:
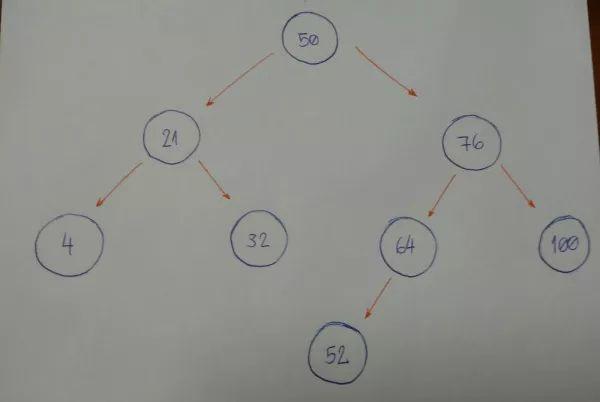
发现规律了么?像开车一样,从根结点驶入,待插入值大于当前结点值向右开否则向左开知道找到空位停车入库。(嘀嘀嘀,老司机)
代码实现也很简单:

这个算法最牛逼的地方在于他的递归部分,你知道是哪几行吗?
结点检索
其实结合我们的插入操作,检索的方法就显而易见,依旧从根结点开始,小于对应结点值左转,大于右转,等于报告找到,走到叶子结点都没找到 gg,就报没有该元素。例如我们想知道下图中有没有52这个值:
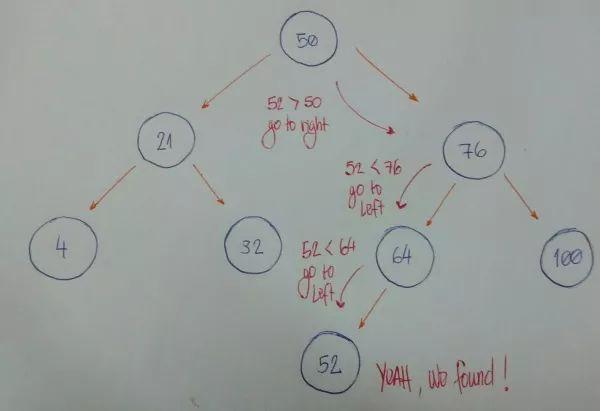
代码如下:

删除: 移除并重构
删除操作要更复杂一些,因为要处理三种不同情况:
情景 #1:叶子结点

是最简单的情况,直接删除就好.
情景 #2:只有左孩子或右孩子

该情景等价于链表上的结点删除,把当前结点删除并让其子结点替换自己原来位置。
情景 #3:同时具有左右孩子的结点

找到该结点右子树中最小值所在的结点,剔除要删除的当前结点并把最小值结点提升到空缺位置。
一些别的操作
清零:将三个属性全部置None即可。

找到最小值:从根节点开始,一直左转,直到找不到任何结点为止,此时我们就找到了最小值。

恭喜你学完本篇内容!数据结构中的树的内容大致如此,赶紧收藏起来吧
(文章来源:优达学城)


