在本文中,我们将介绍以下回归算法:线性回归、Robust 回归、Ridge 回归、LASSO 回归、Elastic Net、多项式回归、多层感知机、随机森林回归和支持向量机。除此以外,本文还将介绍用于评估回归模型的最常用指标,包括均方误差 (MSE)、均方根误差 (RMSE) 和平均绝对误差 (MAE)。
线性回归是机器学习中最简单的算法,它可以通过不同的方式进行训练。 在本文中,我们将介绍以下回归算法:线性回归、Robust 回归、Ridge 回归、LASSO 回归、Elastic Net、多项式回归、多层感知机、随机森林回归和支持向量机。除此以外,本文还将介绍用于评估回归模型的最常用指标,包括均方误差 (MSE)、均方根误差 (RMSE) 和平均绝对误差 (MAE)。

导入库和读取数据
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import hvplot.pandas
%matplotlib inline
sns.set_style("whitegrid") plt.style.use("fivethirtyeight")
USAhousing = pd.read_csv('../usa-housing/USA_Housing.csv') USAhousing.head()1.2.3.4.5.6.7.8.9.10.11.12.探索性数据分析 (EDA)
下一步将创建一些简单的图表来检查数据。 进行EDA将帮助我们熟悉数据和获得数据的信息,尤其是对回归模型影响最大的异常值。
USAhousing.info() <class 'pandas.core.frame.DataFrame'> RangeIndex: 5000 entries, 0 to 4999 Data columns (total 7 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 Avg. Area Income 5000 non-null float64 1 Avg. Area House Age 5000 non-null float64 2 Avg. Area Number of Rooms 5000 non-null float64 3 Avg. Area Number of Bedrooms 5000 non-null float64 4 Area Population 5000 non-null float64 5 Price 5000 non-null float64 6 Address 5000 non-null object dtypes: float64(6), object(1) memory usage: 273.6+ KB1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.
查看数据集的描述
USAhousing.describe()1.
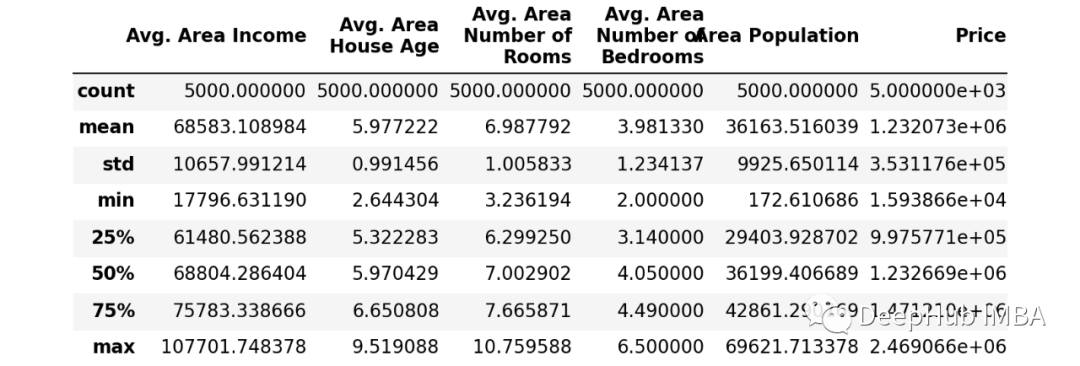
训练前的准备
我们将从训练一个线性回归模型开始,训练之前需要确定数据的特征和目标,训练的特征的 X ,目标变量的 y ,在本例中我们的目标为 Price 列。
之后,将数据分成训练集和测试集。 我们将在训练集上训练我们的模型,然后使用测试集来评估模型。
from sklearn.model_selection import train_test_split X = USAhousing[['Avg. Area Income', 'Avg. Area House Age', 'Avg. Area Number of Rooms', 'Avg. Area Number of Bedrooms', 'Area Population']] y = USAhousing['Price'] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)1.2.3.4.5.6.7.
为了评估回归模型还创建了一些辅助函数。
from sklearn import metrics
from sklearn.model_selection import cross_val_score
def cross_val(model): pred = cross_val_score(model, X, y, cv=10) return pred.mean()
def print_evaluate(true, predicted):
mae = metrics.mean_absolute_error(true, predicted) mse = metrics.mean_squared_error(true, predicted) rmse = np.sqrt(metrics.mean_squared_error(true, predicted)) r2_square = metrics.r2_score(true, predicted) print('MAE:', mae) print('MSE:', mse) print('RMSE:', rmse) print('R2 Square', r2_square) print('__________________________________')
def evaluate(true, predicted): mae = metrics.mean_absolute_error(true, predicted) mse = metrics.mean_squared_error(true, predicted) rmse = np.sqrt(metrics.mean_squared_error(true, predicted)) r2_square = metrics.r2_score(true, predicted) return mae, mse, rmse, r2_square1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.训练回归模型
对于线性回归而言,一般都会有以下的假设:
线性假设:线性回归假设输入和输出之间的关系是线性的。所以可能需要转换数据以使关系线性化(例如,指数关系的对数转换)。
去除噪音:线性回归假设您的输入和输出变量没有噪声。这对于输出变量最重要,如果可能希望删除输出变量 (y) 中的异常值。
去除共线性:当具有高度相关的输入变量时,线性回归将会过拟合。需要将输入数据进行相关性计算并删除最相关的。
高斯分布:如果输入和输出变量具有高斯分布,线性回归将会做出更可靠的预测。对于分布的转换可以对变量使用变换(例如 log 或 BoxCox)以使它们的分布看起来更像高斯分布。
对数据进行处理:使用标准化或归一化重新调整输入变量,线性回归通常会做出更可靠的预测。
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
pipeline = Pipeline([
('std_scalar', StandardScaler())
])
X_train = pipeline.fit_transform(X_train) X_test = pipeline.transform(X_test)1.2.3.4.5.6.7.8.9.下面我们开始进行回归回归算法的示例
1、线性回归和评价指标
from sklearn.linear_model import LinearRegression lin_reg = LinearRegression(normalize=True) lin_reg.fit(X_train,y_train)1.2.3.4.
有了第一个模型,那么就要知道评价模型的指标,以下是回归问题的三个常见评估指标:
平均绝对误差 (MAE) 是误差绝对值的平均值:
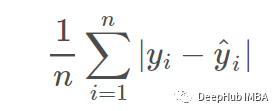
均方误差 (MSE) 是均方误差的平均值:
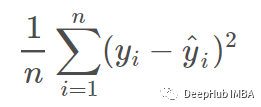
均方根误差 (RMSE) 是均方误差的平方根:
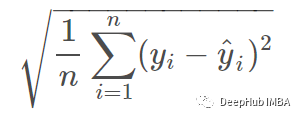
这三个指标中:
MAE 是最容易理解的,因为它是平均误差。
MSE 比 MAE 更受欢迎,因为 MSE “惩罚”更大的错误,这在现实世界中往往很有用。
RMSE 比 MSE 更受欢迎,因为 RMSE 可以用“y”单位解释
这些都是损失函数,我们的训练目标就是最小化他们。
test_pred = lin_reg.predict(X_test) train_pred = lin_reg.predict(X_train)
print('Test set evaluation:\n_____________________________________') print_evaluate(y_test, test_pred) print('Train set evaluation:\n_____________________________________') print_evaluate(y_train, train_pred)
results_df = pd.DataFrame( data=[["Linear Regression", *evaluate(y_test, test_pred) , cross_val(LinearRegression())]], columns=['Model', 'MAE', 'MSE', 'RMSE', 'R2 Square', "Cross Validation"])
Test set evaluation: _____________________________________
MAE: 81135.56609336878
MSE: 10068422551.40088
RMSE: 100341.52954485436
R2 Square 0.9146818498754016
__________________________________
Train set evaluation: _____________________________________
MAE: 81480.49973174892
MSE: 10287043161.197224
RMSE: 101425.06180031257
R2 Square 0.9192986579075526
__________________________________1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.2、Robust回归
Robust回归是一种回归分析形式,它的目标是克服传统参数和非参数方法的一些局限性,旨在不受基础数据生成过程违反回归假设的过度影响。
当数据包含异常值时,则会考虑Robust回归。 在存在异常值的情况下,最小二乘估计效率低下并且可能存在偏差。 因为最小二乘预测被拖向离群值,并且因为估计的方差被人为夸大,结果是离群值可以被掩盖了。
随机样本共识——RANSAC
随机样本共识 (RANSAC) 是一种迭代方法,它从一组观察到的包含异常值的数据中估计数学模型的参数,而异常值不会对估计值产生影响。 因此它也可以理解为一种异常值检测方法。
一个基本的假设是,数据由“内值”和“异常值”组成,“内值”即数据的分布可以用一组模型参数来解释,但可能受噪声影响,“异常值”是不符合模型的数据。RANSAC还假设,给定一组(通常很小)内点,存在一个程序可以估计模型的参数,以最优地解释或拟合该数据。
from sklearn.linear_model import RANSACRegressor
model = RANSACRegressor(base_estimator=LinearRegression(), max_trials=100) model.fit(X_train, y_train)
test_pred = model.predict(X_test) train_pred = model.predict(X_train)
print('Test set evaluation:\n_____________________________________') print_evaluate(y_test, test_pred) print('====================================') print('Train set evaluation:\n_____________________________________') print_evaluate(y_train, train_pred)
results_df_2 = pd.DataFrame( data=[["Robust Regression", *evaluate(y_test, test_pred) , cross_val(RANSACRegressor())]], columns=['Model', 'MAE', 'MSE', 'RMSE', 'R2 Square', "Cross Validation"]
)
results_df = results_df.append(results_df_2, ignore_index=True)
Test set evaluation: _____________________________________
MAE: 84645.31069259303
MSE: 10996805871.555056
RMSE: 104865.65630155115
R2 Square 0.9068148829222649
__________________________________
====================================
Train set evaluation: _____________________________________
MAE: 84956.48056962446
MSE: 11363196455.35414
RMSE: 106598.29480509592
R2 Square 0.9108562888249323
_________________________________1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.3、Ridge回归
Ridge回归通过对系数的大小施加惩罚来解决普通最小二乘法的一些问题。 Ridge系数最小化惩罚残差平方和
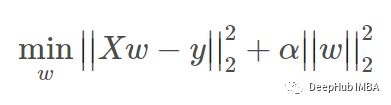
alpha >= 0 是控制收缩量的复杂性参数:alpha 值越大,收缩量越大,因此系数对共线性的鲁棒性更强。
Ridge回归是一个 L2 惩罚模型。 将权重的平方和添加到最小二乘成本函数。
from sklearn.linear_model import Ridge
model = Ridge(alpha=100, solver='cholesky', tol=0.0001, random_state=42) model.fit(X_train, y_train) pred = model.predict(X_test)
test_pred = model.predict(X_test) train_pred = model.predict(X_train)
print('Test set evaluation:\n_____________________________________') print_evaluate(y_test, test_pred) print('====================================') print('Train set evaluation:\n_____________________________________') print_evaluate(y_train, train_pred)
results_df_2 = pd.DataFrame( data=[["Ridge Regression", *evaluate(y_test, test_pred) , cross_val(Ridge())]], columns=['Model', 'MAE', 'MSE', 'RMSE', 'R2 Square', "Cross Validation"]
)
results_df = results_df.append(results_df_2, ignore_index=True)
Test set evaluation: _____________________________________
MAE: 81428.64835535336
MSE: 10153269900.892609
RMSE: 100763.43533689494
R2 Square 0.9139628674464607
__________________________________
====================================
Train set evaluation: _____________________________________
MAE: 81972.39058585509
MSE: 10382929615.14346
RMSE: 101896.66145239233
R2 Square 0.9185464334441484
__________________________________1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.4、LASSO 回归
LASSO 回归是一种估计稀疏系数的线性模型。 在数学上,它由一个用 L1 先验作为正则化器训练的线性模型组成。 最小化的目标函数是:
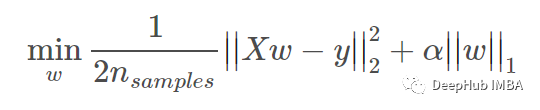
from sklearn.linear_model import Lasso
model = Lasso(alpha=0.1, precompute=True,
# warm_start=True, positive=True, selection='random', random_state=42) model.fit(X_train, y_train)
test_pred = model.predict(X_test) train_pred = model.predict(X_train)
print('Test set evaluation:\n_____________________________________') print_evaluate(y_test, test_pred) print('====================================') print('Train set evaluation:\n_____________________________________') print_evaluate(y_train, train_pred)
results_df_2 = pd.DataFrame( data=[["Lasso Regression", *evaluate(y_test, test_pred) , cross_val(Lasso())]], columns=['Model', 'MAE', 'MSE', 'RMSE', 'R2 Square', "Cross Validation"]
)
results_df = results_df.append(results_df_2, ignore_index=True)
Test set evaluation: _____________________________________
MAE: 81135.6985172622
MSE: 10068453390.364521
RMSE: 100341.68321472648
R2 Square 0.914681588551116
__________________________________
====================================
Train set evaluation: _____________________________________
MAE: 81480.63002185506
MSE: 10287043196.634295
RMSE: 101425.0619750084
R2 Square 0.9192986576295505
__________________________________1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.5、Elastic Net
Elastic Net 使用 L1 和 L2 先验作为正则化器进行训练。 这种组合允许学习一个稀疏模型,其中很少有像 Lasso 那样的非零权重,同时仍然保持 Ridge 的正则化属性。
当多个特征相互关联时,Elastic Net络很有用。 Lasso 可能会随机选择关联特征其中之一,而 Elastic Net 可能会同时选择两者。 Elastic Net最小化的目标函数是:
from sklearn.linear_model import ElasticNet
model = ElasticNet(alpha=0.1, l1_ratio=0.9, selection='random', random_state=42) model.fit(X_train, y_train)
test_pred = model.predict(X_test) train_pred = model.predict(X_train)
print('Test set evaluation:\n_____________________________________') print_evaluate(y_test, test_pred) print('====================================') print('Train set evaluation:\n_____________________________________') print_evaluate(y_train, train_pred)
results_df_2 = pd.DataFrame( data=[["Elastic Net Regression", *evaluate(y_test, test_pred) , cross_val(ElasticNet())]], columns=['Model', 'MAE', 'MSE', 'RMSE', 'R2 Square', "Cross Validation"]
)
results_df = results_df.append(results_df_2, ignore_index=True)
Test set evaluation: _____________________________________
MAE: 81184.43147330945
MSE: 10078050168.470106
RMSE: 100389.49232100991
R2 Square 0.9146002670381437
__________________________________
====================================
Train set evaluation: _____________________________________
MAE: 81577.88831531754
MSE: 10299274948.101461
RMSE: 101485.34351373829
R2 Square 0.9192027001474953
__________________________________1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.6、多项式回归
机器学习中的一种常见模式是使用在数据的非线性函数上训练的线性模型。 这种方法保持了线性方法通常快速的性能,同时允许它们适应更广泛的数据。
可以通过从系数构造多项式特征来扩展简单的线性回归。 在标准线性回归中,可能有一个看起来像这样的二维数据模型:
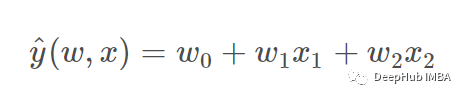
如果我们想对数据拟合抛物面而不是平面,我们可以将特征组合成二阶多项式,使模型看起来像这样:
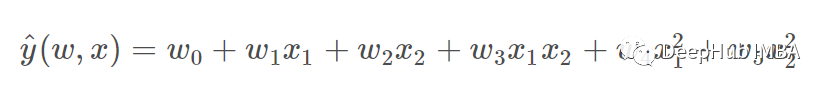
这仍然是一个线性模型:那么如果我们创建一个新的变量
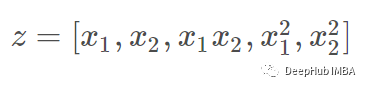
通过重新标记数据,那么公式可以写成
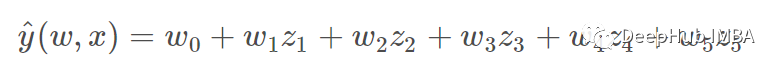
可以看到到生成的多项式回归属于上面的同一类线性模型(即模型在 w 中是线性的),并且可以通过相同的技术求解。 通过考虑使用这些基函数构建的高维空间内的线性拟合,该模型可以灵活地拟合更广泛的数据范围。
from sklearn.preprocessing import PolynomialFeatures
poly_reg = PolynomialFeatures(degree=2)
X_train_2_d = poly_reg.fit_transform(X_train) X_test_2_d = poly_reg.transform(X_test)
lin_reg = LinearRegression(normalize=True) lin_reg.fit(X_train_2_d,y_train)
test_pred = lin_reg.predict(X_test_2_d) train_pred = lin_reg.predict(X_train_2_d)
print('Test set evaluation:\n_____________________________________') print_evaluate(y_test, test_pred) print('====================================') print('Train set evaluation:\n_____________________________________') print_evaluate(y_train, train_pred)
results_df_2 = pd.DataFrame( data=[["Polynomail Regression", *evaluate(y_test, test_pred), 0]], columns=['Model', 'MAE', 'MSE', 'RMSE', 'R2 Square', 'Cross Validation']
)
results_df = results_df.append(results_df_2, ignore_index=True)
Test set evaluation: _____________________________________
MAE: 81174.51844119698
MSE: 10081983997.620703
RMSE: 100409.0832426066
R2 Square 0.9145669324195059
__________________________________
====================================
Train set evaluation: _____________________________________
MAE: 81363.0618562117
MSE: 10266487151.007816
RMSE: 101323.67517519198
R2 Square 0.9194599187853729
__________________________________1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.7、随机梯度下降
梯度下降是一种非常通用的优化算法,能够为各种问题找到最佳解决方案。 梯度下降的一般思想是迭代地调整参数以最小化成本函数。 梯度下降测量误差函数相对于参数向量的局部梯度,它沿着梯度下降的方向前进。 一旦梯度为零,就达到了最小值。
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(n_iter_no_change=250, penalty=None, eta0=0.0001, max_iter=100000) sgd_reg.fit(X_train, y_train)
test_pred = sgd_reg.predict(X_test) train_pred = sgd_reg.predict(X_train)
print('Test set evaluation:\n_____________________________________') print_evaluate(y_test, test_pred) print('====================================') print('Train set evaluation:\n_____________________________________') print_evaluate(y_train, train_pred)
results_df_2 = pd.DataFrame( data=[["Stochastic Gradient Descent", *evaluate(y_test, test_pred), 0]], columns=['Model', 'MAE', 'MSE', 'RMSE', 'R2 Square', 'Cross Validation']
)
results_df = results_df.append(results_df_2, ignore_index=True)
Test set evaluation: _____________________________________
MAE: 81135.56682170597
MSE: 10068422777.172981
RMSE: 100341.53066987259
R2 Square 0.914681847962246
__________________________________
====================================
Train set evaluation: _____________________________________
MAE: 81480.49901528798
MSE: 10287043161.228634
RMSE: 101425.06180046742
R2 Square 0.9192986579073061
__________________________________1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.8、多层感知机
多层感知机相对于简单回归任务的好处是简单的线性回归模型只能学习特征和目标之间的线性关系,因此无法学习复杂的非线性关系。 由于每一层都存在激活函数,多层感知机有能力学习特征和目标之间的复杂关系。
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Input, Dense, Activation, Dropout
from tensorflow.keras.optimizers import Adam
X_train = np.array(X_train) X_test = np.array(X_test) y_train = np.array(y_train) y_test = np.array(y_test)
model = Sequential()
model.add(Dense(X_train.shape[1], activation='relu')) model.add(Dense(32, activation='relu'))
# model.add(Dropout(0.2))
model.add(Dense(64, activation='relu'))
# model.add(Dropout(0.2))
model.add(Dense(128, activation='relu'))
# model.add(Dropout(0.2))
model.add(Dense(512, activation='relu')) model.add(Dropout(0.1)) model.add(Dense(1))
model.compile(optimizer=Adam(0.00001), loss='mse')
r = model.fit(X_train, y_train, validation_data=(X_test,y_test), batch_size=1, epochs=100) pd.DataFrame({'True Values': y_test, 'Predicted Values': pred}).hvplot.scatter(x='True Values', y='Predicted Values') pd.DataFrame(r.history)1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.
pd.DataFrame(r.history).hvplot.line(y=['loss', 'val_loss'])1.
test_pred = model.predict(X_test) train_pred = model.predict(X_train)
print('Test set evaluation:\n_____________________________________') print_evaluate(y_test, test_pred)
print('Train set evaluation:\n_____________________________________') print_evaluate(y_train, train_pred)
results_df_2 = pd.DataFrame( data=[["Artficial Neural Network", *evaluate(y_test, test_pred), 0]], columns=['Model', 'MAE', 'MSE', 'RMSE', 'R2 Square', 'Cross Validation']
)
results_df = results_df.append(results_df_2, ignore_index=True)
Test set evaluation: _____________________________________
MAE: 101035.09313018023
MSE: 16331712517.46175
RMSE: 127795.58880282899
R2 Square 0.8616077649459881
__________________________________
Train set evaluation: _____________________________________
MAE: 102671.5714851714
MSE: 17107402549.511665
RMSE: 130795.2695991398
R2 Square 0.8657932776379376
__________________________________1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.9、随机森林回归
from sklearn.ensemble import RandomForestRegressor
rf_reg = RandomForestRegressor(n_estimators=1000) rf_reg.fit(X_train, y_train)
test_pred = rf_reg.predict(X_test) train_pred = rf_reg.predict(X_train)
print('Test set evaluation:\n_____________________________________') print_evaluate(y_test, test_pred)
print('Train set evaluation:\n_____________________________________') print_evaluate(y_train, train_pred)
results_df_2 = pd.DataFrame( data=[["Random Forest Regressor", *evaluate(y_test, test_pred), 0]], columns=['Model', 'MAE', 'MSE', 'RMSE', 'R2 Square', 'Cross Validation']
)
results_df = results_df.append(results_df_2, ignore_index=True)
Test set evaluation: _____________________________________
MAE: 94032.15903928125
MSE: 14073007326.955029
RMSE: 118629.70676417871
R2 Square 0.8807476597554337
__________________________________
Train set evaluation: _____________________________________
MAE: 35289.68268023927
MSE: 1979246136.9966476
RMSE: 44488.71921056671
R2 Square 0.9844729124701823
__________________________________1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.10、支持向量机
from sklearn.svm import SVR
svm_reg = SVR(kernel='rbf', C=1000000, epsilon=0.001) svm_reg.fit(X_train, y_train)
test_pred = svm_reg.predict(X_test) train_pred = svm_reg.predict(X_train)
print('Test set evaluation:\n_____________________________________') print_evaluate(y_test, test_pred)
print('Train set evaluation:\n_____________________________________') print_evaluate(y_train, train_pred)
results_df_2 = pd.DataFrame( data=[["SVM Regressor", *evaluate(y_test, test_pred), 0]], columns=['Model', 'MAE', 'MSE', 'RMSE', 'R2 Square', 'Cross Validation']
)
results_df = results_df.append(results_df_2, ignore_index=True)
Test set evaluation: _____________________________________
MAE: 87205.73051021634
MSE: 11720932765.275513
RMSE: 108263.25676458987
R2 Square 0.9006787511983232
__________________________________
Train set evaluation: _____________________________________
MAE: 73692.5684807321
MSE: 9363827731.411337
RMSE: 96766.87310960986
R2 Square 0.9265412370487783
__________________________________1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.结果对比
以上就是我们常见的10个回归算法,下面看看结果的对比
results_df1.
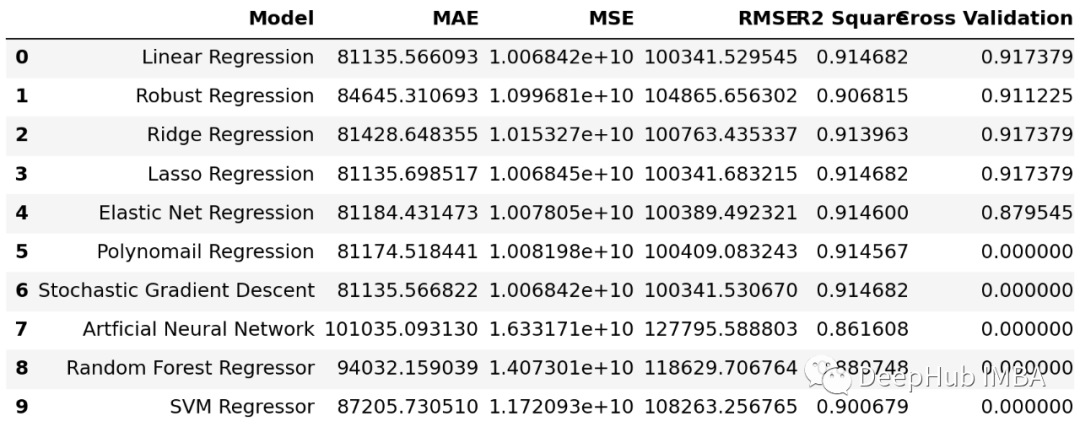
results_df.set_index('Model', inplace=True) results_df['R2 Square'].plot(kind='barh', figsize=(12, 8))1.2.
可以看到,虽然本例的差别很小(这是因为数据集的原因),但是每个算法还是有细微的差别的,我们可以根据不同的实际情况选择表现较好的算法。
总结
在本文中,我们介绍了机器学习中的常见的线性回归算法包括:
常见的线性回归模型(Ridge、Lasso、ElasticNet……)
模型使用的方法
采用学习算法对模型中的系数进行估计
如何评估线性回归模型
责任编辑:华轩来源: DeepHub IMBA


