前言
最近为了巩固一下自己的算法基础,又把算法书里的基本算法刷了一遍, 特地总结一下前端工程师需要了解的排序算法和搜索算法知识,虽然还有很多高深算法需要了解, 但是基础还是要好好巩固一下的.本文将以图文的形式为大家介绍如下算法知识,希望在读完之后大家能有所收获:
冒泡排序及其优化
选择排序
插入排序
归并排序
快速排序
顺序搜索
二分搜索
正文
我想对于每个前端工程师来说, 最头疼的就是算法问题, 但是算法往往也是衡量一个人编程能力的一个很重要的指标.目前很多主流框架和库都应用了大量的算法和设计模式,为了让自己的段位更高,我们只能不断的"打怪"(也就是刷算法)升级,才能成为"最强王者".
其实前端发展这么多年, 越来越偏向于精细化开发, 很多超级应用(比如淘宝,微信)都在追求极致的用户体验, 时间就是金钱,这要求工程师们不能像以前那样,开发的程序只要能用就行, 我们往往还要进行更加细致的测试(包括单元测试, 性能测试等),就拿排序来说, 对于大规模数据量的排序, 我们采用冒泡排序肯定是要被疯狂吐槽的,因为冒泡排序的性能极差(复杂度为O(n^2).在真实项目中我们往往不会采用冒泡排序,
有详细介绍. 接下来就让我们来一起学习如何实现文章开头的几个常用排序和搜索算法吧.
1. 冒泡排序及其优化
我们在学排序算法时, 最容易掌握的就是冒泡排序, 因为其实现起来非常简单,但是从运行性能的角度来看, 它却是性能最差的一个.
冒泡排序的实现思路是比较任何两个相邻的项, 如果前者比后者大, 则将它们互换位置.
为了更方便的展示冒泡排序的过程和性能测试,笔者先写几个工具方法,分别为动态生成指定个数的随机数组, 生成元素位置序列的方法,代码如下:
// 生成指定个数的随机数组
const generateArr = (num = 10) => {
let arr = []
for(let i = 0; i< num; i++) {
let item = Math.floor(Math.random() * (num + 1))
arr.push(item)
}
return arr}// 生成指定个数的元素x轴坐标
const generateArrPosX = (n= 10, w = 6, m = 6) => {
let pos = []
for(let i = 0; i< n; i++) {
let item = (w + m) * i
pos.push(item)
}
return pos}1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.有了以上两个方法,我们就可以生成任意个数的数组以及数组项坐标了,这两个方法接下来我们会用到.
我们来直接写个乞丐版的冒泡排序算法:
bubbleSort(arr = []) {
let len = arr.length
for(let i = 0; i< len; i++) {
for(let j = 0; j < len - 1; j++) {
if(arr[j] > arr[j+1]) {
// 置换 [arr[j], arr[j+1]] = [arr[j+1], arr[j]]
}
}
}
return arr }1.2.3.4.5.6.7.8.9.10.11.12.接下来我们来测试一下, 我们用generateArr方法生成60个数组项的数组, 并动态生成元素坐标:
// 生成坐标 const pos = generateArrPosX(60) // 生成60个项的数组 const arr = generateArr(60)1.2.3.4.
执行代码后会生成下图随机节点结构:
有关css部分这里就不介绍了,大家可以自己实现.接下来我们就可以测试我们上面写的冒泡排序了,当我们点击排序时,结果如下:
可以看到数组已按照顺序排好了,我们可以使用console.time来测量代码执行所用的时间,上面"乞丐版"冒泡排序耗时为0.2890625ms.
我们深入分析代码就可以知道两层for循环排序导致了很多多余的排序,如果我们从内循环减去外循环中已跑过的轮数,就可以避免内循环中不必要的比较,所以我们代码优化如下:
// 冒泡排序优化版
bubbleSort(arr = []) {
let len = arr.length
// 优化
for(let i = 0; i< len; i++) {
for(let j = 0; j < len - 1 - i; j++) {
if(arr[j] > arr[j+1]) {
// 置换
[arr[j], arr[j+1]] = [arr[j+1], arr[j]]
}
}
}
return arr
}1.2.3.4.5.6.7.8.9.10.11.12.13.14.经过优化的冒泡排序耗时:0.279052734375ms, 比之前稍微好了一丢丢, 但仍然不是推荐的排序算法.
2. 选择排序
选择排序的思路是找到数据结构中的最小值并将其放置在第一位,接着找到第二个最小值并将其放到第二位,依次类推.
我们还是按照之前的模式,生成一个60项的数组, 如下:
选择排序代码如下:
selectionSort(arr) {
let len = arr.length,
indexMin
for(let i = 0; i< len -1; i++) {
indexMin = i
for(let j = i; j < len; j++){
if(arr[indexMin] > arr[j]) {
indexMin = j }
}
if(i !== indexMin) {
[arr[i], arr[indexMin]] = [arr[indexMin], arr[i]]
}
}
return arr}1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.点击排序时, 结果如下:
说明代码运行正常, 可以实现排序, 控制台耗时为: 0.13720703125ms, 明显比冒泡排序性能要好.
3. 插入排序
插入排序的思路是每次排一个数组项,假定第一项已经排序,接着它和第二项比较, 决定第二项的位置, 然后接着用同样的方式决定第三项的位置, 依次类推, 最终将整个数组从小到大依次排序.
代码如下:
insertionSort(arr) {
let len = arr.length,
j,
temp;
for(let i = 1; i< len; i++) {
j = i
temp = arr[i]
while(j > 0 && arr[j-1] > temp) {
arr[j] = arr[j-1]
j--
}
arr[j] = temp;
}
}1.2.3.4.5.6.7.8.9.10.11.12.13.14.执行结果如下:
控制台打印耗时为:0.09912109375ms.
4. 归并排序
归并排序算法性能比以上三者都好, 可以在实际项目中投入使用,但实现方式相对复杂.
归并排序是一种分治算法,其思想是将原始数组切分成较小的数组,直到每个小数组只有一个元素,接着将小数组归并成较大的数组,最后变成一个排序完成的大数组。
其实现过程如下图所示:
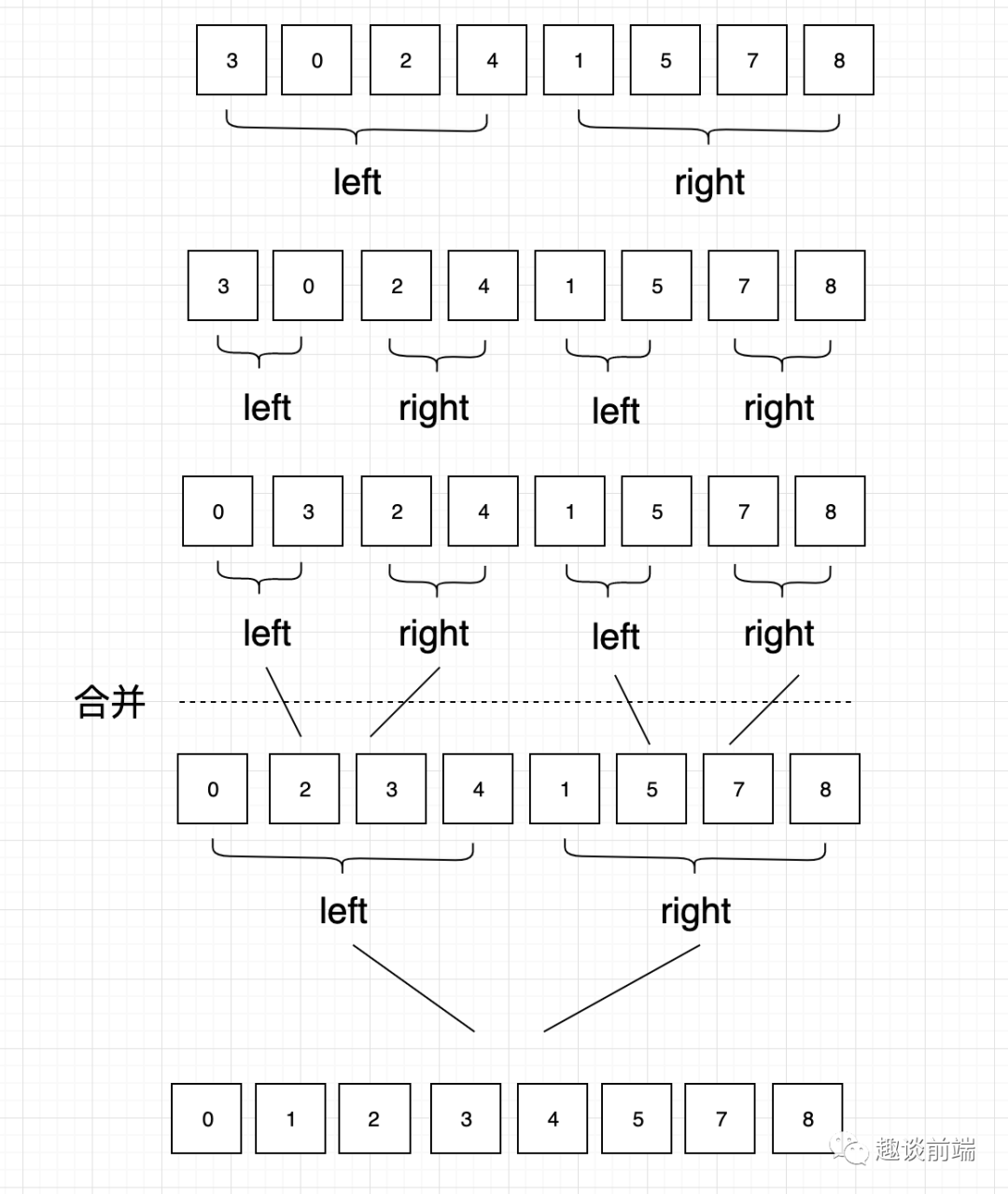
为了实现该方法我们需要准备一个合并函数和一个递归函数,具体实现如下代码:
// 归并排序
mergeSortRec(arr) {
let len = arr.length
if(len === 1) {
return arr }
let mid = Math.floor(len / 2),
left = arr.slice(0, mid),
right = arr.slice(mid, len)
return merge(mergeSortRec(left), mergeSortRec(right))}// 合并方法
merge(left, right) {
let result = []
l = 0,
r = 0;
while(l < left.length && r < right) {
if(left[l] < right(r)) {
result.push(left[l++])
}else {
result.push(right[r++])
}
}
while(l < left.length) {
result.push(left[l++])
}
while(r < right.length) {
result.push(right[r++])
}
return result}1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.以上代码中的递归作用是将一个大数组划分为多个小数组直到只有一项,然后再逐层进行合并排序。如果有不理解的可以和笔者交流或者结合笔者画的草图进行理解。
5. 快速排序
快速排序是目前比较常用的排序算法,它的复杂度为O(nlog^n),并且它的性能比其他复杂度为O(nlog^n)的好,也是采用分治的思想,将原始数组进行划分,由于快速排序实现起来比较复杂,这里讲一下思路:
从数组中选择中间项作为主元
创建两个指针,左边一个指向数组第一项,右边一个指向数组最后一项,移动左指针直到我们找到一个比主元大的元素,移动右指针直到找到一个比主元小的元素,然后交换它们的位置,重复此过程直到左指针超过了右指针
算法对划分后的小数组重复1,2步骤,直到数组完全排序完成。
代码如下:
// 快速排序
quickSort(arr, left, right) {
let index
if(arr.length > 1) {
index = partition(arr, left, right)
if(left < index - 1) {
quickSort(arr, left, index -1)
}
if(index < right) {
quickSort(arr, index, right)
}
}
}// 划分流程
partition(arr, left, right) {
let part = arr[Math,floor((right + left) / 2)],
i = left,
j = right
while(i <= j) {
while(arr[i] < part) {
i++
}
while(arr[j] > part) {
j--
}
if(i <= j) {
// 置换 [arr[i], arr[j]] = [arr[j], arr[i]]
i++
j--
}
}
return i}1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.7. 顺序搜索
搜索算法也是我们经常用到的算法之一,比如我们需要查找某个用户或者某条数据,不管是在前端还是在后端,都会使用搜索算法。我们先来介绍最简单也是效率最低的顺序搜索,其主要思想是将每一个数据结构中的元素和我们要查询的元素做比较,然后返回指定元素的索引。
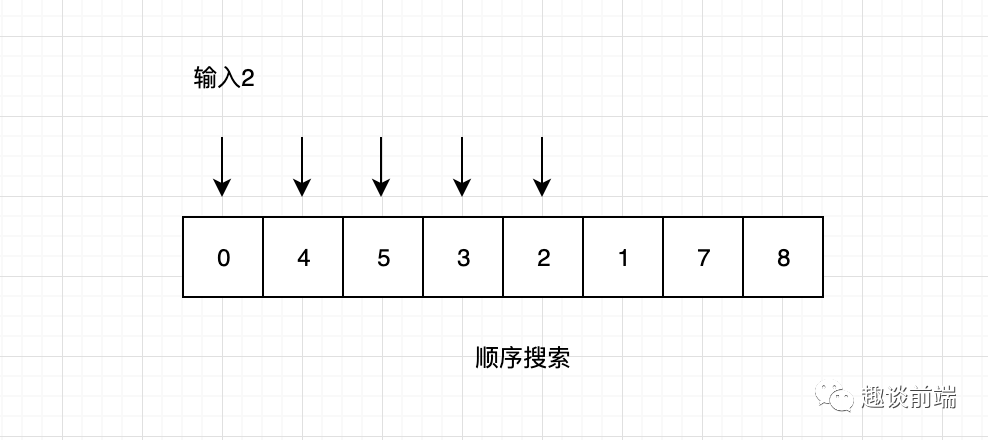
之所以说顺序搜索效率低是因为每次都要从数组的头部开始查询,直到查找到要搜索的值,整体查询不够灵活和动态性。顺序搜索代码实现如下:
sequentialSearch(arr, item) {
for(let i = 0; i< arr.length; i++) {
if(item === arr[i]) {
return i }
}
return -1}1.2.3.4.5.6.7.8.接下来我们看下面一种比较常用和灵活的搜索算法——二分搜索。
8. 二分搜索
二分搜索的思想有点“投机学”的意思,但是它是一种有理论依据的“投机学”。首先它要求被搜索的数据结构已排序,其次进行如下步骤:
找出数组的中间值
如果中间值是待搜索的值,那么直接返回中间值的索引
如果待搜索的值比中间值小,则返回步骤1,将区间范围缩小,在中间值左边的子数组中继续搜索
如果待搜索的值比选中的值大,则返回步骤1,将区间范围缩小,在中间值右边的子数组中继续搜索
如果没有搜到,则返回-1
为了方便理解笔者画了如下草图:
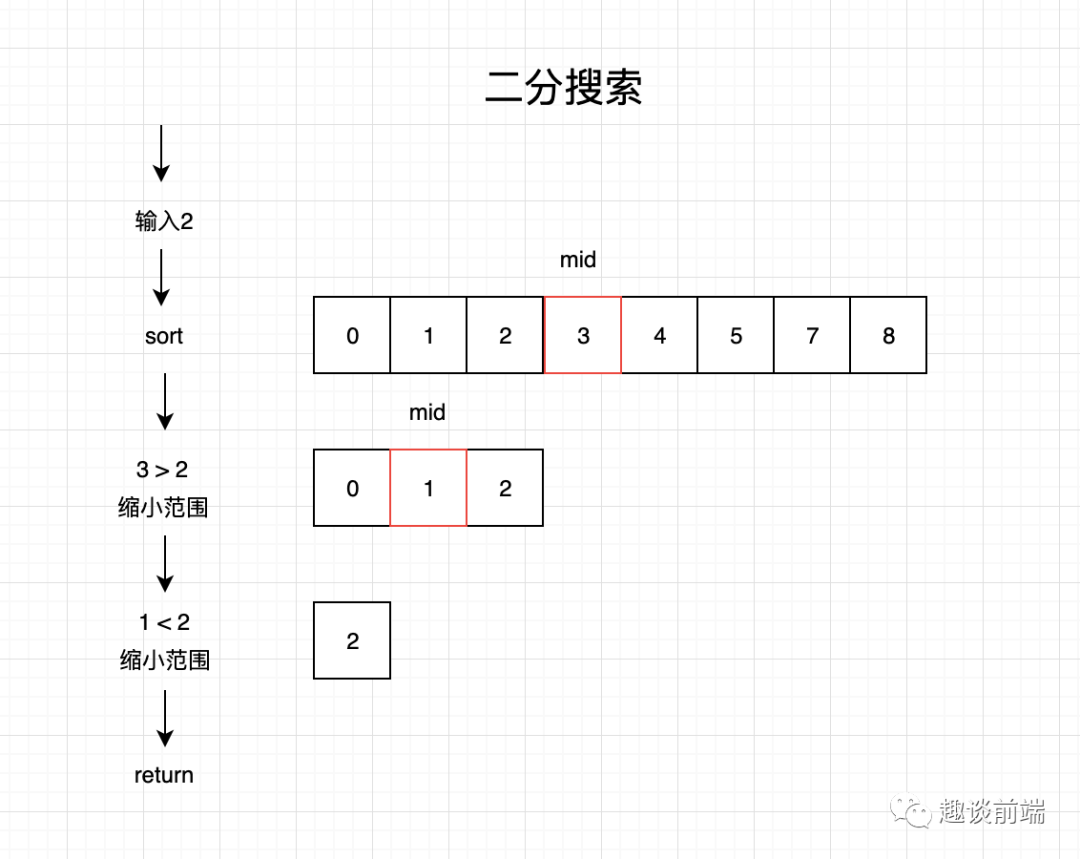
由上图大家可以很容易的理解二分搜索的实现过程,接下来我们看下代码实现:
binarySearch(arr, item) {
// 调用排序算法先对数据进行排序
this.quickSort(arr)
let min = 0,
max = arr.length - 1,
mid,
el
while(min <= max) {
mid = Math.floor((min + max) / 2)
el = arr[mid]
if(el < item) {
min = mid + 1
}else if(el > item) {
max = mid -1
}else {
return mid }
}
return -1
}1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.其实还有很多搜索算法,笔者在js基本搜索算法实现与170万条数据下的性能测试有具体介绍。
参考文献:Learning JavaScript Data Structures and Algorithms


